Teorema de Pitágoras (Lo que si debes saber)

 Teorema de Pitágoras

Es una herramienta que permite resolver diferentes problemáticas, resaltando su papel de instrumento útil, para la solución. En el que se estudian distintas demostraciones del Teorema de Pitágoras, considerándolo como objeto de estudio y analizando cuáles serán los conocimientos necesarios para su desarrollo. Este tema corresponde a 3° grado de secundaria

Lo que si deben saber

• Definir los conceptos básicos del teorema de Pitágoras (Hipotenusa, cateteo opuesto, cateto adyacente)

Hipotenusa: Se denomina hipotenusa al lado mayor de triángulo rectángulo, el lado opuesto al ángulo recto.

Cateto opuesto: Es el que esta opuesto o enfrente del ángulo.

Cateto adyacente: Es el lado que está siempre alado del ángulo

•  Definir para que nos sirve el teorema de Pitágoras:

Podíamos utilizar el teorema de Pitágoras para obtener una longitud lateral faltante en un triángulo rectángulo, si sabíamos las otras dos longitudes. Ahora podemos relacionar las medidas de ángulos con las longitudes laterales del triángulo rectángulo. Esto nos permite determinar las dos longitudes laterales faltantes cuando sólo conocemos una longitud y la medida de un ángulo agudo. Podemos también obtener las medidas de ángulos agudos en un triángulo rectángulo por medio de las longitudes de cualesquiera de sus lados

• Conocer el tipo de triangulo que vamos a utilizar, en este caso “el triángulo rectángulo” (sus propiedades, por qué se le llama así, el número de lados que tiene, con que lados vamos a trabajar, etc)

El triángulo que se utiliza es el rectángulo. La principal característica del triángulo es que, tiene un lado de mayor longitud (llamado hipotenusa) y otros dos denominados catetos cuya unión forma el ángulo recto. Otro detalle a notar es que cualquier cuadrado separado en dos por alguna de sus diagonales se divide en dos triángulos rectángulos

Propiedades: 

• Tiene dos ángulos agudos.

• La hipotenusa es mayor que cualquiera de los catetos.

• La longitud del cuadrado de la hipotenusa es igual a la suma de la longitud de los cuadrado de los catetos (teorema de Pitágoras)

• La suma de la longitud de la hipotenusa y el diámetro de un círculo inscrito en el triángulo es igual a la suma de la longitud de los catetos.

• La mediana de la hipotenusa descompone un triángulo rectángulo escaleno en dos triángulos: uno obtusángulo y otro acutángulo, no congruentes pero equivalentes.

• La mediana de la hipotenusa de un triángulo rectángulo isósceles lo descompone en dos triángulos rectángulos isósceles congruentes y equivalentes.

• La mediana que parte del ángulo recto es igual a la mitad de la hipotenusa.

• La altura que parte del vértice del ángulo recto, coincide con un cateto, con tal de considerar al otro cateto como una base

 

• Fórmula para encontrar cada uno de sus  lados

Como se sabe el valor de la hipotenusa la encontramos de la siguiente manera

𝑐² = √𝑏² + 𝑎²

Esta fórmula sale porque al momento de resolver √𝑏² + 𝑎² y sacarle raíz, nos da el resultado de 𝑐², es decir que la suma de los dos catetos es igual a la hipotenusa.

Para sacar el valor del cateto A:

𝑎² = √𝑐² − 𝑏²
y para sacar el valor del cateto B: 

 𝑏² = √𝑐² − 𝑎²

Las funciones trigonométricas con relación al teorema de Pitágoras:

Las razones trigonométricas se utilizan fundamentalmente en la solución de triángulos rectángulos, recordando que todo triangulo rectángulo tiene un angulo de 90° y sus angulos interiores suman 180°.

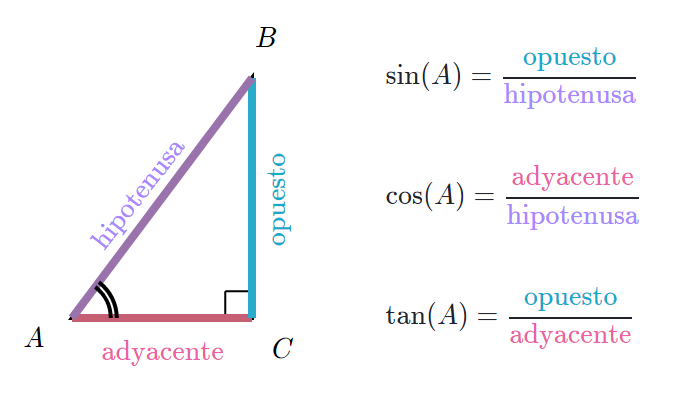
Se definen las razones trigonometrícas de la siguiente manera:

Ejemplo:

1.- Resolver el siguiente triangulo cuando los catetos miden 3cm y 4 cm

Para obtener los ángulos a y β, podemos hacerlo de la siguiente manera:
Tan= 3/4

α= 𝑡𝑎𝑛⁻¹ 0.75

α= 36.87°

y como

α+β+90°=180 despejando
β=180°-90°-36.87°
β= 53.13

• Se usa el llamado “Triple pitagórico” :
  

Un triple pitagórico tiene tres enteros positivos a, b y c, tales que
a2 + b2 = c2.. En otras palabras, un triple pitagórico representa las longitudes de los lados de un triángulo rectángulo en el que los tres lados tienen longitudes enteras.1 

Este triple se suele escribir (a, b, c). Algunos ejemplos conocidos son (3, 4, 5) y (5, 12, 13).